(今はまだ一番下にあるスライドからコピペしただけな段階で詳しい説明などは後日追加します)
はじめに
この記事ではなんで人類が多様体なんてものを考えだしたかその歴史的,数学的な流れを丁寧に追ってみたいと思います.なぜ多様体は重要かと困惑している方々の理解の助けになればと思います.
ここでは二次元の場合に話を限って考えます.
$\def\A{\mathbb{A}}
\def\B{\mathbb{B}}
\def\C{\mathbb{C}}
\def\F{\mathbb{F}}
\def\G{\mathbb{G}}
\def\H{\mathbb{H}}
\def\K{\mathbb{K}}
\def\M{\mathbb{M}}
\def\N{\mathbb{N}}
\def\O{\mathcal{O}}
\def\P{\mathbb{P}}
\def\Q{\mathbb{Q}}
\def\R{\mathbb{R}}
\def\T{\mathbb{T}}
\def\Z{\mathbb{Z}}
\def\mf{\mathfrak}
\def\mc{\mathcal}
\DeclareMathOperator{\cl}{Cl}
\DeclareMathOperator{\spec}{Spec}
\DeclareMathOperator{\vol}{vol}
\DeclareMathOperator{\aut}{Aut}
\DeclareMathOperator{\gal}{Gal}
\DeclareMathOperator{\ker}{Ker}
\newcommand{\dprod}{\displaystyle\prod}
\renewcommand{\set}[2]{\left\{ #1 \mathrel{} \middle| \mathrel{} #2 \right\}}$
「幾何学」とは何か
おなじみの平面幾何学とはどういうものだったか?
基本的な考察対象:点,直線,三角形,円,多角形,...
基本的な考察内容:交わるかどうか,角度,面積,比,...
参考:幾何学は紀元前からの長い歴史を持っている(リンド・パピルス(B.C.1650,インド),ピタゴラス,アルキメデス,エラトステネス...)
→ずっと$X=\R^2$(ユークリッド平面)という空間の中で考えてきた.
→別の空間$X$の中で考えたらどうなるだろうか?
「直線」,「平行」という用語の振り返り
ここでは$X$を一般の空間としよう.$X$内の曲線$C$の長さを$L(C)$で表すことにする.
点$P,Q\in X$を用意する.$P$から$Q$へと至る曲線$C$のうち$L(C)$を最小にするようなものを「$P,Q$を結ぶ線分(あるいは直線)」という.曲線$C$の上のどんな二点$P,Q\in C$をとっても$C$の$P$から$Q$へと至る部分が「$P,Q$を結ぶ線分」であるとき,$C$を直線という.
二点$P,Q\in X$の間の「距離」$d(P,Q)$とは何か検討し直してみよう.
$d(P,Q):=( \set{L(C)}{\text{$C$は$P,Q$を結ぶ曲線}}\text{の下限})$
つまり「最短距離」のイメージ.
直線$l,l'$はそれらが交点を持たないとき平行であるという.
これらの定義は今後非常に重要になるのでよくよく抑えておいてほしい(特に赤字部分).
$X=\R^2$(平面)で,$P=(a,b),Q=(a',b')$と書かれるとき
$d(P,Q)=\sqrt{(a-a')^2+(b-b')^2}$
$S^2$(球面)上の直線

$X=S^2$(球面)における直線は大円(球の中心を通る平面で切ったときの断面の境界)(立派な定理)
→$X=S^2$(球面)において,平行な直線のペアは存在しない!
地面に”平行に”(正確には接ベクトルが平行ということ)2つ直線を引いて地球一周するとそれらは必ずどこかで交わる!
$S^2$における「三角形」
まず「三角形」という用語を振り返ろう.
空間$X$においてどの2つも平行でないような3つの直線に囲まれた(フチも込めた)領域を三角形という(ただし全てが一点で交わるような状況は考えない).

$\mathfrak{h}$(上半平面)上の幾何学

$X=\mathfrak{h}$(上半平面(=平面$\R^2$の$y>0$の部分))ではおなじみの距離($d_{\R^2}(P,Q)=\sqrt{(a-a')^2+(b-b')^2}\ (P=(a,b),Q=(a',b'))$)とは違うポアンカレの距離というものを考える(後で出てくる).
(二次元の)空間$X$内の(区分的に滑らかな)曲線$C:x=x(t),y=y(t)\ (t\in [0,1])$の長さが$L(C)$で与えられるとき,二点$P,Q\in X$の間の「距離」$d_{X}(P,Q)$として次のように定義されるものを考えることが出来る:

上の状況において
$L(C):=\displaystyle\int_0^1 \frac{1}{y(t)}\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt$
と定めたときに生じる距離$d_{\mathfrak{h}}$のことをポアンカレの距離という.
(参考:おなじみのユークリッド距離$d_{\R^2}$は上の積分で$\frac{1}{y(t)}$の部分を消したもの)
$\mathfrak{h}$(上半平面)上の直線
ポアンカレの距離で考えたとき,$X=\mathfrak{h}$(上半平面)における直線は以下の2パターン(これも立派な定理):
・$x$軸に中心を持つ半円
・$y$軸に平行な半直線

どんな直線$l$と($l$の上にない)点$P$に対しても$l$に平行で$P$を通るような直線は無数に存在する!
$\mathfrak{h}$における「三角形」
空間$X$においてどの2つも平行でないような3つの直線に囲まれた(フチも込めた)領域を三角形という(ただし全てが一点で交わるような状況は考えない).

空間$X$の曲がり具合を表す量
曲率というものを定義する際,単純な発想としては局所的に円とみなして定義することが出来るが,ガウスはそれとは違うものとして数学的にとても筋の良いガウス曲率という偉大な基準を考えた(cf.ガウスの驚異の定理).定義は難しいので省略する.
(”曲がり具合”という直感に合致しない例もあるので注意されたい(円柱のガウス曲率は0).)
例:$S^2,\R^2,\mathfrak{h}$のガウス曲率

ガウス曲率の偉大さ
これはつまり長さに関して2つの”幾何学$X,Y$が等しい”ならばそのガウス曲率は変わらないということである.
→ガウス曲率はそれが$X$を外側から眺めることなく$X$の上に住んでいる人間から決定できてしまうという「($X$における)内在性」を持っている!
これの意味は例えば$X=S^2$なら通常はより大きな$U=\R^3$という大きな空間に埋め込んで考えるが,$X=S^2$のガウス曲率は$U$の幾何学的情報とは無関係に決まってしまうということである.これは$X=S^2$そのものを(”$U$の中の図形”ではなく)”空間”とみなすべきだ,という深い示唆をしていると取ることも出来るだろう.
この定理により,人類はロケットに乗ることなく地球が平面とは違う形をしていることを証明できてしまう.
空間$X$を一つ固定し,その中での事象を考える.$X$の各点$P$におけるガウス曲率$K(P)$が全て同じ$K(P)=K$(定曲率)なとき,以下が成り立つ.
$X$における三角形$\Delta$は各頂点の角度が$\alpha,\beta,\gamma$であるとする.ここで$\Delta$の面積を$S$とするとき,
$KS=\alpha+\beta+\gamma-\pi$
(定曲率でないときにももちろん定理は成立し,左辺は各点のガウス曲率$K(P)$と$\Delta$によって決まる量であるが少し高度な対象となる)
ガウス・ボンネの定理より以下が分かる:
上の状況において,
(1) $X=S^2$(球面)のとき$K=p\ (p>0)$(正の実数)とすると
$S=\frac{1}{p}(\alpha+\beta+\gamma-\pi)$
(2) $X=\R^2$(平面)のとき
$\alpha+\beta+\gamma=\pi$
(3) $X=\mathfrak{h}$(上半平面)のとき$K=-p\ (p>0)$(負の実数)とすると
$S=\frac{1}{p}(\pi-\alpha-\beta-\gamma)$
このことから,三角形の内角の和は$X=S^2$(球面)においては$\pi$より大きく,$X=\mathfrak{h}$(上半平面)においては$\pi$より小さいことがわかる!
まとめ
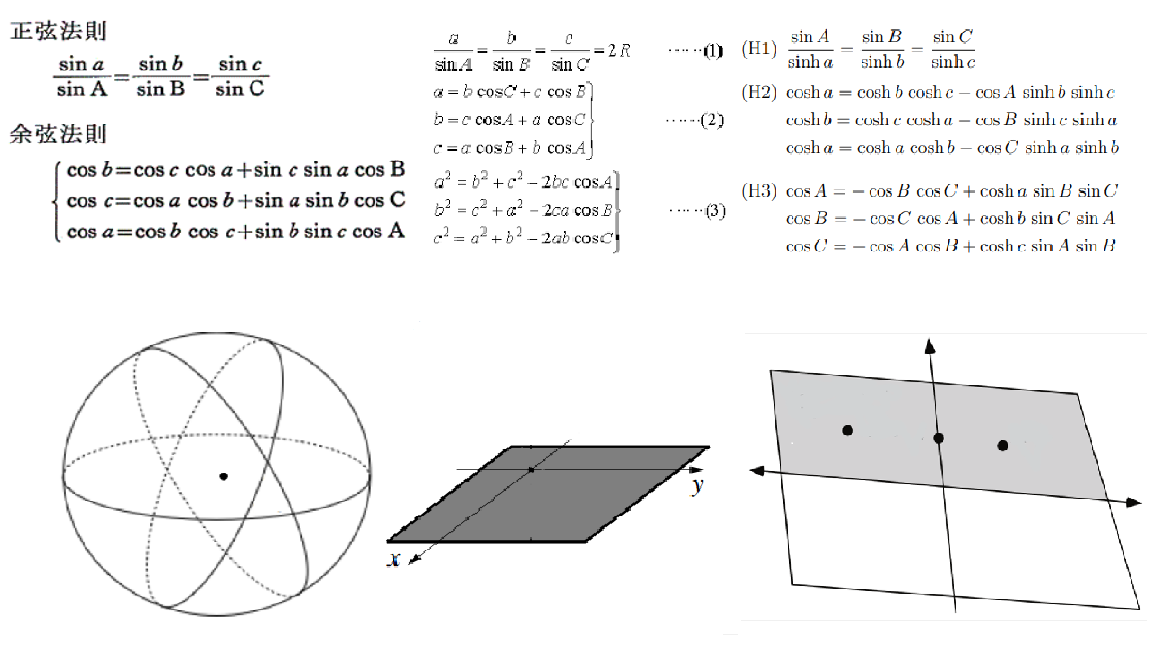
空間$X$の幾何学的構造(ガウス曲率$K$,距離$d$など)がその上の幾何学に(本質的かつ)多大な影響を及ぼしている!(19世紀頃:ガウス,リーマン,クライン...)
展望
$X$をもっと色んな”空間”に変えて”$X$-幾何学”(その上の幾何学)を考えてみたい!
→人類が$X$自体を考察対象にし始める
→どういった数学的対象$X$であれば”空間”と呼べるか?
→「多様体(manifold)」の概念(リーマンがそのアイデアを提唱(1854),ワイルやホイットニーらが厳密な定義を確立(1936))
→現代幾何学の始まり:
基本的な考察対象:多様体$M$,その上の関数や微分形式,...
基本的な考察内容:微分同相による分類問題,埋め込み問題,...
人類が新たに見えたもの:ストークスの定理の真の姿,ド・ラーム理論,サーストンの幾何化予想($\Rightarrow$ ポアンカレ予想!),ミルナーの7次元エキゾチック球面,...
物理学への応用:一般相対性理論(宇宙を(4次元擬リーマン)多様体と考え,その上に物理学を展開することで辻褄が合った)
Q.多様体論はどこで教えてくれるの?
→数学科(と一部の物理学科)だけ!
この記事はとある高校で講演するとき用意したスライドを元にしています:
